What do the Parthenon, a sunflower, a nautilus shell and the Mona Lisa have in common?
The answer is 1.618033
“Liber Abacci”
In 1202, Leonardo of Pisa, better known as Leonardo Fibonacci, published “Liber Abacci” where the use of the decimal system was elucidated. In his work, he wanted his readers to learn to use the decimal system. In the text, Fibonacci wondered how fast rabbits would reproduce under ideal conditions. Thus, Fibonacci posed the problem as follows:
“With a single pair of rabbits, both members ready to breed after a month of existence and give birth to a new partner after a month of gestation. How many pairs of rabbits will be there after one year?
Fibonacci rabbits
At the end of the first month, the original pair is ready to procreate, but there remains a single partner. At the end of the second month, there will be the original couple and their first daughter. At the end of the third month, there will be the original first couple, which is now ready to procreate, and a second pair-daughter. At the end of the fourth month, there will be the original and first pair of daughters and the second pair of daughters, who are ready to procreate. The succession of pairs of rabbits then is: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… This sequence would come to be known as the “Fibonacci sequence,” but what do the Fibonacci numbers have to do with 1.618033? It turns out that if you take one of the Fibonacci numbers (either succession) and that number is divided by its immediate past, as progress is made in the succession, the ratio will go closer and closer to the before mentioned number also called… “The golden ratio”.
The sequence of numbers by Fibonacci “ends” in the infinite … and it is called φ “Phi” the number of delicacy and beauty, synonymous of balance and harmony, but be careful, do not confuse it with π (Pi) which is the ratio between the length of a circle to its diameter and is frequently used in mathematics, physics and engineering. The numerical value, truncated to its preliminary figures, 3.1416 is as follows: 3.14159265358979323846∞ and represents the area, considered the most perfect geometric body, the sphere. Pi and Phi have in common that both belong to the set of irrational numbers and those quantities have infinite nonperiodic decimal places, which therefore cannot be expressed as fractions.
MATH, ART AND THE DIVINE
Luca Pacioli
The first historical manifestation recorded, dates from the fifteenth century when the Franciscan friar and the mathematician precursor of calculating odds Luca Pacioli (1445 – 1517) analyzed in its writing “De Divina Proportione” (From the Divine Proportion) the so-called golden number. Highly influenced by the idea that every new discovery should be adapted to the beliefs of the Catholic church, he called it “divine proportion” since according to him, phi had a correspondence with the holy trinity; ie “the same proportion will always be between three terms, and never more or less.”
His writings date from between 1496 and 1498; the subject of his dissertation was divided in 3 parts. Polygons and perspective used by the painters of the Quattrocento(1) in its second, architectural ideas of Vitruvius (2) and platonic solids or regular(3). To illustrate this, he commissioned drawings from Leonardo da Vinci, which at the time was part of the court of Ludovico Sforza.
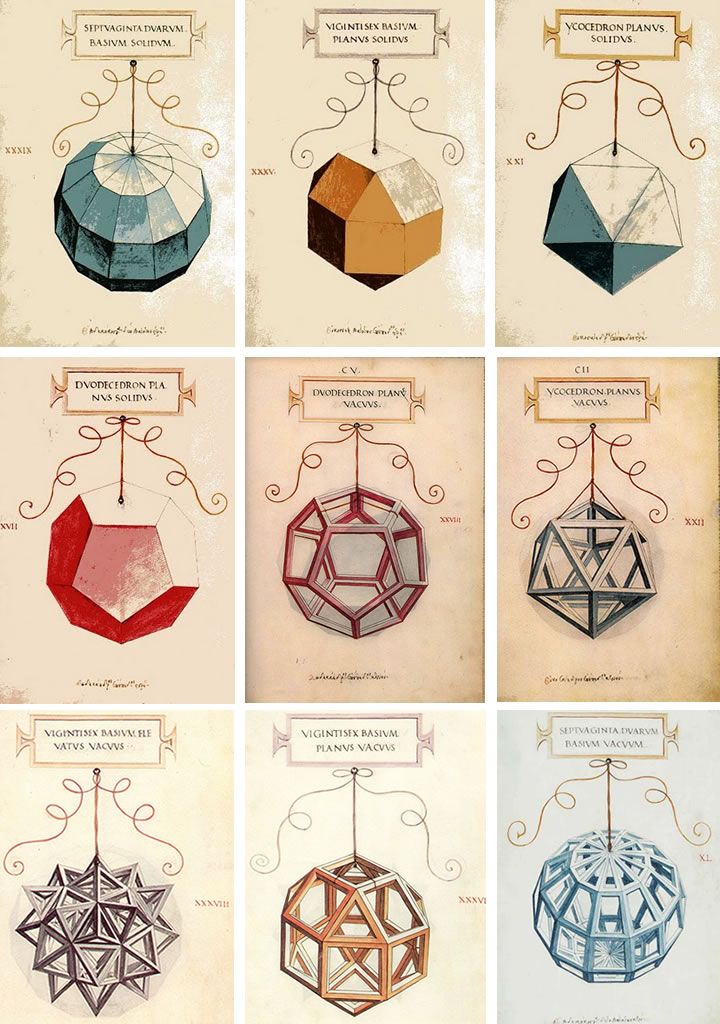
(1)Compendio Divina Proportione (2)Summa de arithmetica, geometría, proportioni et proportionalita precipitevolissimevolmente (3)De quinque corporibus regularibus
Although Luca Pacioli called it “divine proportion” it was Leonardo da Vinci who christened this number as the “golden number,” influenced by two extraordinary and true “renaissance men”:
Leon Battista Alberti — priest, personal secretary to three Popes, humanist, architect, scholar, mathematician, poet, cryptographer, linguist, philosopher, musician and archaeologist, and Antonio di Pietro Averlino Filaret, sculptor, engineer, architect and theorist of Renaissance architecture. Da Vinci was convinced that architecture and human anatomy were intrinsically linked. In the 1480´s he delved deeper into this relationship expressed in “Man of Vitrivio” in which he stated:
Man of Vetrivio by Da Vinci
“In the human body, the central part is the navel. For if a man lie on your back, arms and legs outstretched, and a pair of compasses focus on the navel, the fingers and feet will touch the circumference described from the center. And you can also enroll in a square figure.”
Leonardo was obsessed with finding this ratio, which is clearly manifested in his works.
The Last Supper
NATURE AND MATHEMATICS
Same as we can find φ (Phi) in art, we can also find this ubiquitous number in nature. An example is a honeycomb.
Drones are born from unfertilized egg of the queen, so the drone has a mother, but no father. On the contrary, both the queen and the workers are born from eggs fertilized by a male. Therefore, they have a father and mother. Having said this, the family tree of a drone is as follows: 1 mother, 2 grandparents (male and female), 3 great-grandparents (two grandmothers and one grandfather) 5 great-grandparents, 8 great-great-grandparents and so on. If you noticed, the sequence of the family tree of a drone is 1, 1, 2, 3, 5, 8 … ie, the Fibonacci sequence.
Identical pattern of numbers are also found in the spiral of sunflowers, in the number of flower petals, in cauliflower and bananas.
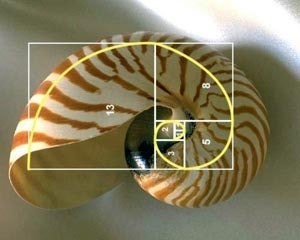
However, in nature, there is no better and clearer example of the golden ratio than the shell of a nautilus, which is the result of a logarithmic spiral that can be drawn with a pencil and a compass.
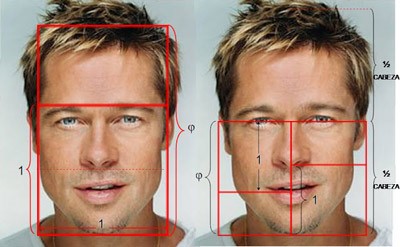
In this example, the numbers are converted into geometric shapes. This examples we see repeated again and again in the universe and even human face… maybe Leonardo was on to something.
THE NUMBER OF GOD
The golden number has astonished and amazed both mystics and mathematicians the same. Fibonacci sequences and their resulting tendency to phi make this subject sound more mystic than mathematical because of its recurring presence in the proportions of the universe. Therefore, many say that the Cosmos has a complex mathematical order, only possible thanks to an intelligent mind, a Creator… God perhaps?
photo: Fotolia
In philosophy great thinkers oriented this belief of mystical transcendence such as Pythagoras and Aristotle, and even in modern times, we find great thinkers as theoretical physicist Michio Kaku, considered one of the most respected and important scientists today and one of the creators and developers of the “string theory,” claims to have created a hypothesis that may point to the existence of God. This information has instituted a stir in the scientific community.
In the words of Michio Kaku:
-“I have concluded that we are in a world made by rules created by a more complex and unthinkable intelligence. Analyzing the behavior of matter at the subatomic scale. Believe me, everything we call chance today will have no sense. To me it is clear that we are in a plane governed by rules created and not determined by universal hazards “.-
Is the “golden number” proof of the existence of an intelligent designer of everything, and whose language is in the mathematics?
The question remains in the air.
J.Urioste
[email protected]
Merida, Yucatan.
April 05 2016
Snakes and Ladders is a column by José E. Urioste, The Yucatan Times CEO and a Business Intelligence professional in the area of Research and Development. He began his training process in mass media writing scripts for radio programs, commercials and advertising campaigns and has contribuited with newspapers, magazines and other media in general on various topics ranging from the professional to the editorial. José is the author of various fiction novels that have been presented in numerous forums and literary competitions, causing much controversy as to their content.
